Pool wars?

Mining pools

Before we can really talk about winners and losers we really need to take a simple look at how mining pools pay out to their miners.

A mining pool needs to use a way to have its contributors demonstrate that they've been working to find Bitcoin blocks. Given that Bitcoin is designed as a trust-less system this isn't a trivial problem. The approach that is taken is to have miners submit "shares" where a share is defined to be a proof-of-work solution towards the Bitcoin block that the pool is trying to find but that doesn't necessarily meet the difficulty requirement for a full Bitcoin block. Shares that don't meet the Bitcoin network's difficulty aren't actually useful (there's no concept of incrementally building a viable solution) but can be used to estimate how much work each pool contributor has performed.

Say, for example, the Bitcoin network has a difficulty of 40B (40,000,000,000) and we have a mining pool that has a nominal 1% of the network. On average the contributors to our pool will find one full block 1.44 times per day (assuming the network isn't growing). To work out who is contributing what, our mining pool might take submissions that are 100k (100,000) times less difficult (400,000 in this case). Now the pool would receive 144,000 submissions per day, of which, on average, 1.44 would find full blocks for the pool. If one miner contributes, say, 1% of our pool's hashing capacity then that miner will be responsible for a nominal 1440 shares per day.

Mining pools use a variety of different schemes to reward contributions but most use some form of paying out rewards from any full Bitcoin block that the pool finds, based on some proportion of the shares submitted beforehand by its participants. Let's assume that we're looking at a reasonably simple case where the payout is proportionate to the number of shares submitted since the pool last found a block. Our pool, on average, finds a block 1.44 times per day and thus receives 100,000 shares between blocks that it finds, of which the last one is the solution to a block. Our 1% miner will have submitted 1000 of these shares and the pool will pay out a proportionate amount of the mined block reward. At its most simplistic the pool might charge 0% fees but, say, keep the transaction fees, so if the block reward is 25 BTC then our 1% miner receives a nominal 0.25 BTC every time the pool finds a block; 0.36 BTC per day.

To the miner this is a far more consistent reward than the one block every 69.4 days that they might hope to achieve on average mining on their own, and carries a much lower variance in terms of potential returns.

We should note that all of the above is a simplification because mining is a Non-Homogeneous Poisson Process and as such all of the numbers are mean values. For example our miner may end up submitting 1050 shares for one block and 950 for the next and 1000 for the one after that; it won't be a consistent 1000 for each.

Block withholding

Block withholding is a scenario in which a miner submits valid lower-difficulty shares but does not submit shares that match full Bitcoin blocks. If they do this then they still receive a proportion of anything else that the pool earns but prevent the pool from claiming the reward for any blocks that they should have contributed. In the case of our hypothetical 1% miner again and pool, they would reduce the pool's income by 1% but would still continue to gain 1% of what the pool did earn. The miner would have harmed the pool by a small amount at a much lower impact to their own returns. The withholding miner does not get to keep the block as pools protect against this!

Intuitively this seems like it would be a bad idea for the miner withholding blocks unless they simply wished to attack the pool. Eyal's paper shows that this isn't necessarily the case.

Let's consider a large-scale example. Imagine that we have a pool with 25% of the network hash rate and it wishes to attack another open pool that has 25% of the network:

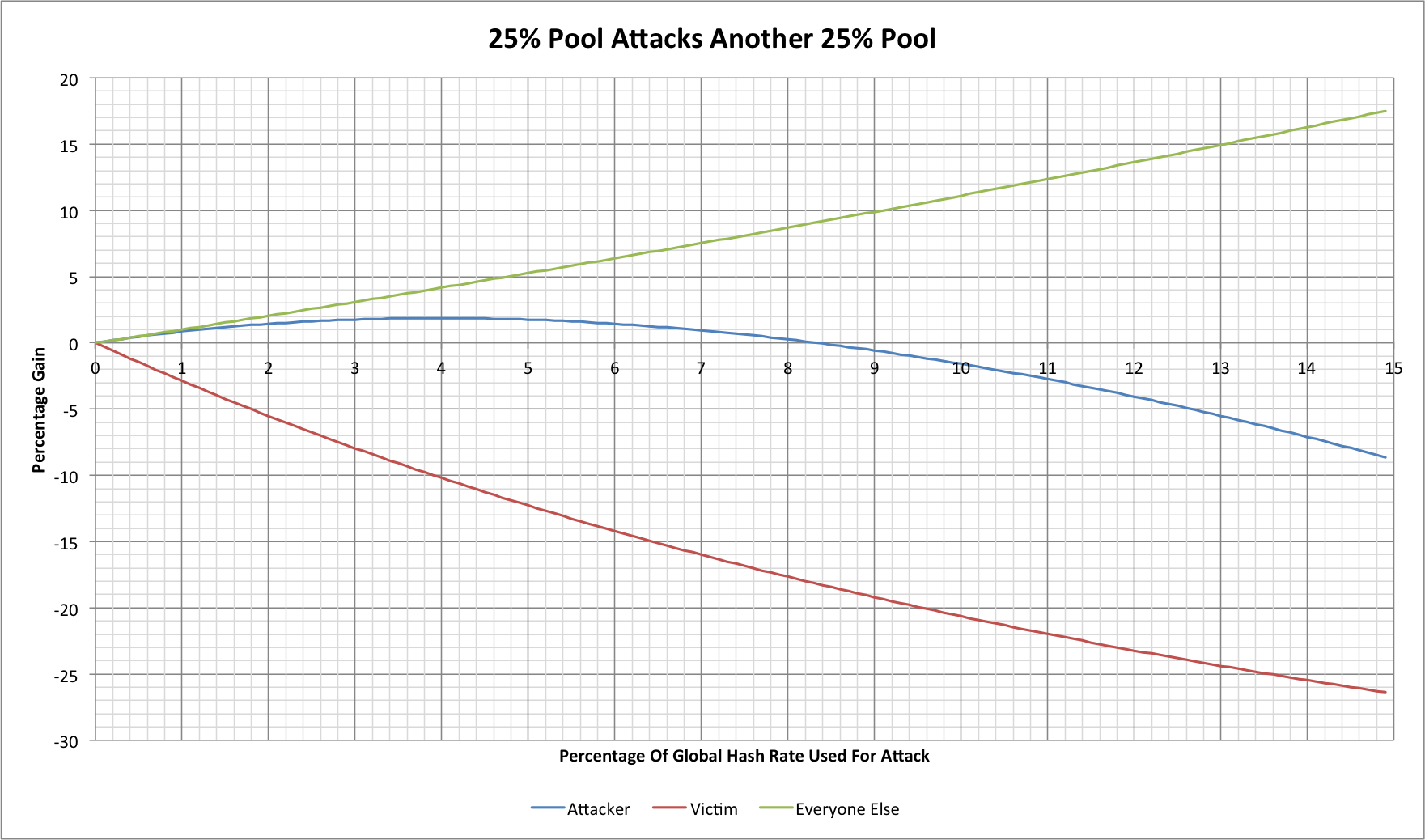
The vertical axis shows the percentage gains that the various participants in the network will see above what they would have seen if no-one was conducting an attack. The horizontal axis shows the percentage of the total network hash rate allocated to the attack. In this case the maximum value would be 25% as that is the total available to the attacker.

There are some very striking trends! First the biggest winners in any such attack are the neutral third parties. The attack removes hashing from the network and so everyone else finds more of the blocks (albeit more slowly until after the next difficulty change reduces the difficulty). The more intriguing aspect is that the attacker also gains financially! At up to 4% of the network hash rate (approximately 16% of the pool's capacity) the attacker achieves a 1.87% increase in their total revenue. At that same 4%, however, our victim has lost 10.2% of their revenue meaning that this has significantly harmed the other miners in the victim pool.

There is an interesting quirk in all of this as regards the operator of the victim pool. If they mine within their own pool then they will also suffer losses from the attack, but if they don't then they may actually see increased income too! The attacker reduces their own hash rate and so the victim pool is actually going to find a larger percentage of the total blocks. In the example above, if the attacker shifts 4% of the total network hash rate to the attack then the victim pool's original 25% is now 26.04% of the network and thus sees a total revenue increase of 4.17%. A pool operator who takes a percentage of mined rewards or takes the transaction fees will actually see a 4.17% increase in their own income even as the victim miners see a significant reduction in theirs.

Smaller scale?

We might now ask what happens if our pools are smaller. Say our attacker has 10% of the network hash rate and our victim has 10%:

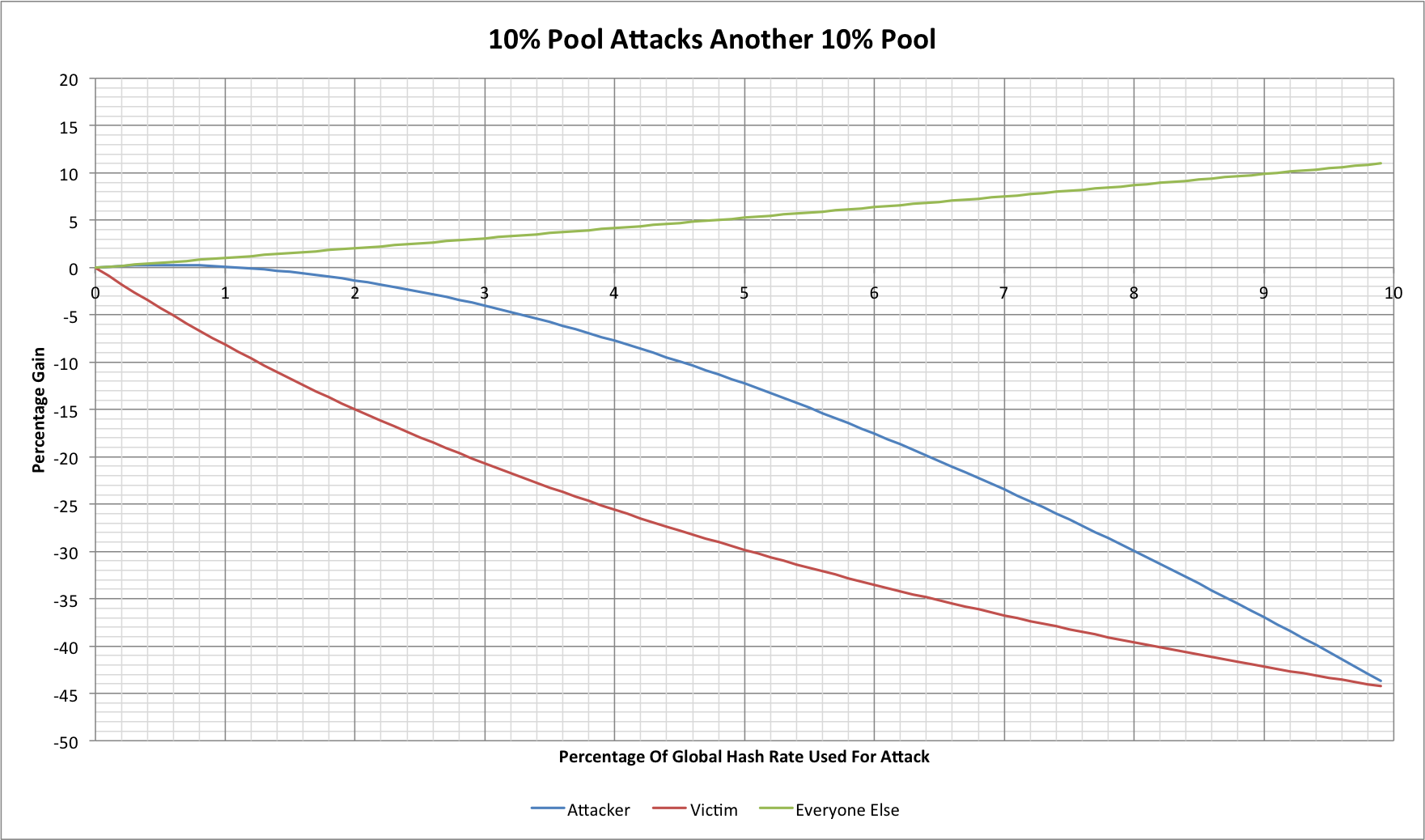
The curves are similar, they're just scaled down. In fact the attacker has less scope to win, achieving a maximum gain of 0.28% when deploying 0.55% of the global hash rate during the attack (approximately 5.5% of the pool's capacity). Conversely though the losses to the victim accumulate faster because a fixed amount of hash rate targeted towards it represents a proportionately larger fraction of the pool's capacity.

If we consider two pools each of which have 1% of the global hashing capacity then things scale even further. There is still a tiny margin for an attacker to see a positive reward but it is only at 0.005% of the global hash rate (approximately 0.5% of the pool's capacity). It's clear that the nominal rewards from this style of attack scale dramatically in percentage terms as the attacker and victim hold larger percentages of the total network capacity.

Scaling effects (part 1)

The scaling effects we've just considered may seem surprising, but a little thought reveals that they are not. The attacker wins by gaining a larger share of the victim pool's revenue and at the same time causes the victim pool to actually still generate more revenue. If the amount of hashing involved in an attack is small, however, then the attacker's switched hashing doesn't affect the global hash rate by very much. The larger the attack, the larger the effect. This has other implications that we will return to later.

Mutually assured destruction?

If one party can attack another then surely the victim might retaliate? There are some wrinkles to this but for now let's just consider that. Here are our original two 25% sized protagonists withholding blocks from each other in similar proportions:

Attacker 1 isn't off the chart here, they're just on the same trend line as our previous victim, now "Attacker 2". Now it's clear that "Everyone Else" would sit back and enjoy the fight. The more the two antogonists contribute to the fight the quicker both lose!

We might assume that the attackers could simply try to harm everyone else too, but the attack only works against open mining pools in which participants can sign up and contribute shares without an element of trust between the mining pool operator and the miners who contribute shares. This is the wrinkle noted above; if our attacker has 25% of the hash rate but operates a private/closed mining pool then the victim cannot retaliate. If the "Everyone Else" capacity is found in closed mining pools then they cannot be victims of this type of attack either.

Big vs little?

We've seen two large pools involved, but what happens with a large attacker and a small open pool?

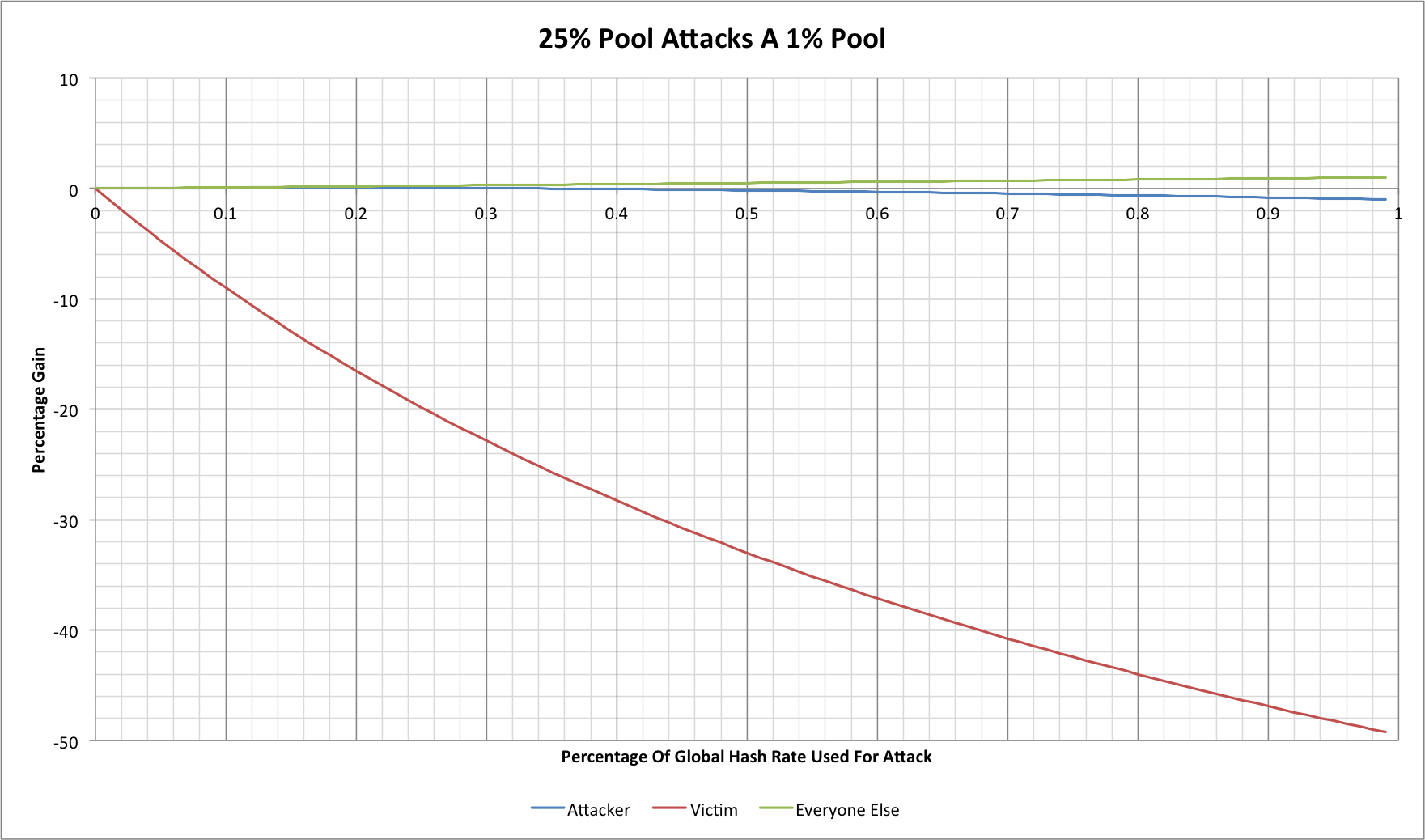
There is a very small period here where the attacker makes a slight gain, but it quickly dissipates. At the point where 0.33% of the global hash rate has been used (1.33% of the pool's total) the attacker is no longer gaining, but the victim pool's miners sees a 25% reduction in revenue. At that sort of loss in revenue it would be likely that miners would start seeking other ways to mine more profitably.

Little vs big?

If this works one way round then can it work the other way round?

Clearly the answer is yes a small attacker can still gain a small amount at the expense of a large victim! It's worth noting though that in order to do this they must use 12.7% of their total hashing capacity to achieve the largest gain and that the gain in question probably isn't sufficient to be worthwhile.

Scaling effects (part 2)

So far what we've seen is that large attackers and large victims result in big gains for attackers and that attackers not operating in open pools cannot be victims of retaliation. We've also seen that small pools can certainly suffer at the hands of large ones but not in ways that are directly profitable to larger pools (other than damaging competitors). It might seem that this is a clear win for small mining pools, but let's not get too hasty! There are (at least) 2 problems:

• Small mining pools suffer from significantly worse reward variances as we've seen before in, "The gambler's guide to Bitcoin mining"
• The block withholding attack scales up by attacking multiple pools!

Let's consider 2 victim mining pools with 12.5% of the total hash rate each, and an attacker that has 25%. Now if our attacker targets each with 2% of the global hash rate then the effects are identical to using 4% to attack one pool with 25% of the total hash rate. Similarly attacking 25 pools with 1% of the global hash rate each and targeting 0.16% at each has the same effect. In fact if an attacker has a reasonable estimate for the hash rate of potential victims then an attack can be made, proportionate to each one's size.

There is a potential problem for would-be attackers though. If two attackers target the same victim with a large enough combined attack then they will actually push the potential gains into negative territory for both of them.

Countermeasures?

The only real way to prevent an attacker or group of attackers from being able to gain from this sort of attack would be to reduce the mining rewards paid by pools for shares rather than for actual full blocks.

In the case of a 10% pool attacking another 10% pool we would require that shares be paid no more than 90% of the total mined reward in order to prevent an attacker from gaining. In the case of a 25% pool attacking another 25% pool then the share-only reward would have to be no more than 75% of the total mined reward while a 40% pool attacking another 40% pool would require that share-only rewards be 60% or less of the total earned.

As we've seen before, though, the problem is that this attack scales so attacking 25 pools of 1% size is the same as attacking one of 25%; the pools couldn't set share payout levels that reduced the vast majority of miners' payouts by 25%, even though a few lucky miners would gain far more for finding full blocks.

Bring on the stealth weapons

In the scenarios we have considered so far our attacker transfers some of their hashing capacity from mining to attacking so that hashing capacity ceases to find blocks that are declared to the rest of the network. With very large pools the loss in hash rate should at least raise some eyebrows, especially if the same hashing capacity didn't reappear somewhere else. With this said, however, statistical variance would certainly mask some of this.

An alternative, however, would be for an attacker to deploy "stealth" hashing. This is hashing capacity that has never been used for conventional mining but is brought online solely to attack open pools. As this capacity would never have contributed to hash rate statistics then it won't be noticed by anyone, potentially including the victim pool, because it can be targeted in small chunks of a few TH/s each.

Let's see what this might look like:

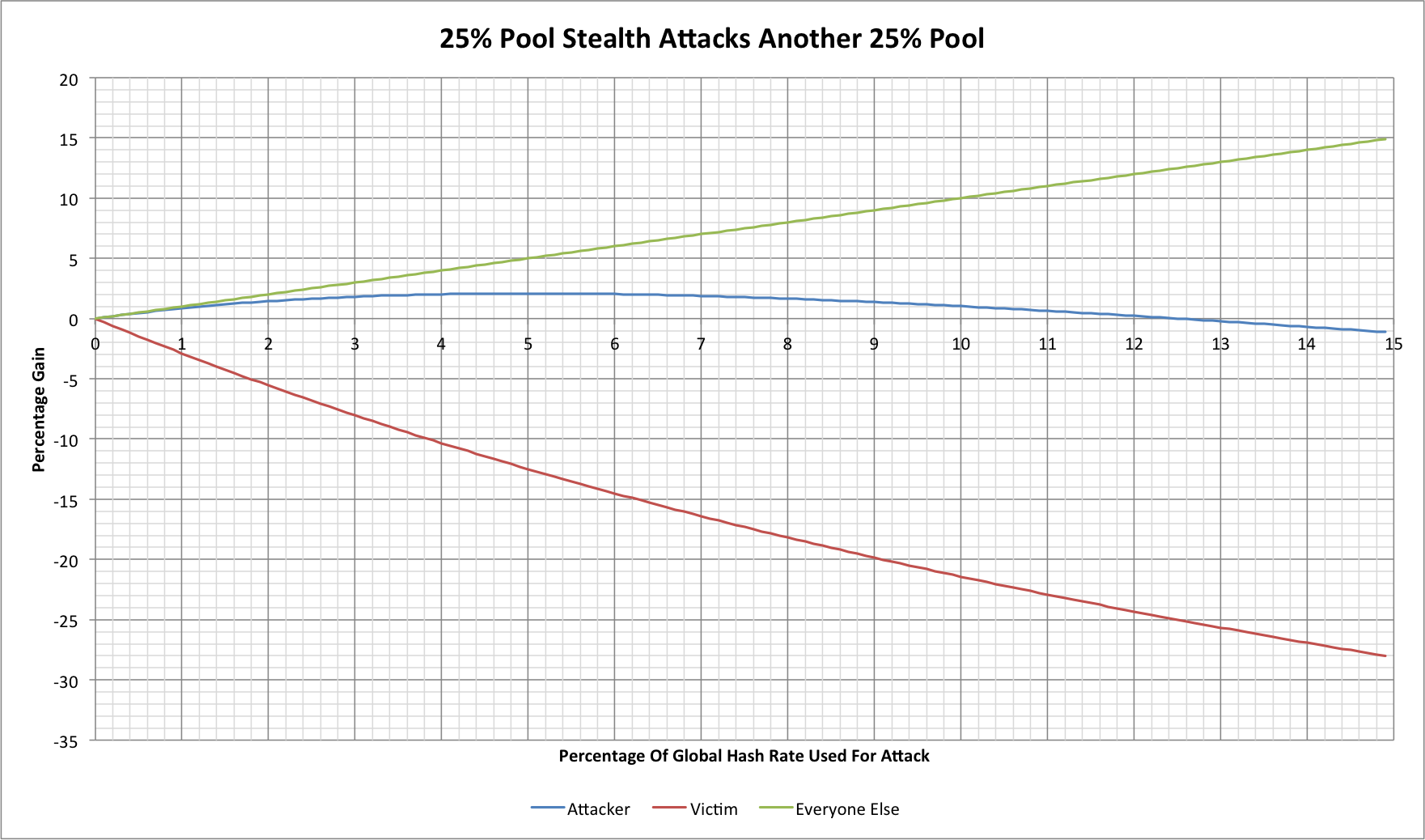
Consider a case where our attacker adds 5% of the useful global hash rate for the purpose of attacks. They now control 28.6% of the total hash rate (their new 5% dilutes their old 25%) but are achieving 2.08% more than their 28.6% would normally achieve. The victim pool (or pools) loses 12.5%, however! Our attacker knows that they have gained but no-one else is any the wiser, while our victim appears to be suffering from bad luck, and it could take months to statistically demonstrate that this wasn't just bad luck in any meaningful way. No external observers would be any the wiser unless the victim pool publishes its share data for analysis (which most pools would probably not wish to do for privacy reasons).

More than just a theory?

Are we actually seeing this style of attack on mining pools already? Realistically unless someone published verifiable details of what they had done then it's probably impossible to tell. Have we seen large-scale attacks? Perhaps not, but as with so many other Bitcoin network statistics there's a lot of room for things to hide!

Source code

This article was written with the help of data from a C language simulation. The data was rendered into charts using Excel. The source code can be found on github: https://github.com/dave-hudson/pool-wars